WordPress へようこそ。こちらは最初の投稿です。編集または削除し、コンテンツ作成を始めてください。
投稿者: valleyin.wp@gmail.com
-
比例とは?
比例という言葉、聞いたことありますか?
「難しい」「聞きたくない」と思っている読者。
このブログを見れば比例が得意になるかもしれませんよ?
日常生活における「比例」
数学は日常生活に置き換えることでより楽しく学ぶことができるかと思います。
では比例は日常生活においてどのような例が見られるか。
お風呂のお湯をためる
お風呂のお湯をためるのは比例の関係になっていることは知っていましたか?
例えばお風呂をためるとき、1分間で10cm高さが上がるとしたら70㎝たまるまで何分かかるか考えてみましょう。
1分間で10cm溜まることがわかっているのであれば、2分後は何cm溜まるかはわかりますよね?
2分後は20cm溜まっていることは明確です。3分後は30㎝になりますよね。時間が2倍になると溜まる量も2倍に、時間が3倍になると溜まる量も3倍に…
ではこれ
 を図で見てみましょう。
を図で見てみましょう。表にまとめてみると以下のようになります。
時間[分] 0 1 2 3 4 5 6 溜まる量[cm] 0 10 20 30 40 50 60 では以上のことから1分間に10㎝お風呂にお湯が溜まることを知っていた場合、70cm溜まるのに何分かかるかはわかりますよね?
お湯を出してから7分待ってあげればお湯は出来上がります。
速さと距離の関係
日常生活において徒歩や自転車、電車、車などを利用して遠い距離を移動していますよね。
では遠い距離を移動をする際には徒歩より車や電車を利用する方が早く目的地に着きますよね?
これも比例です。
では歩いた時と自転車に乗ったときの時間と距離の比較をしてみましょう。
歩く速度を5km/hとし、自転車の速度を10km/hとします。そこで30分ごとに5時間移動します。
ではこれらを図で見てみましょう。

表にまとめてみると以下のようになります。
時間[h] 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 徒歩の(5km/h)
距離[km]0 2.5 5.0 7.5 10.0 12.5 15.0 17.5 20.0 22.5 25.0 自転車の(10km/h)
距離[km]0 5.0 10.0 15.0 20.0 25.0 30.0 35.0 40.0 45.0 50.0 上の表を見ると一目瞭然ですが、速度が速い自転車の方が時間を追うごとに長い距離を移動していることがわかりますね。
比例の性質
以上のことから比例はある値が大きくになるにつれて、他の値もそれい対応して大きくなる。
例えば時間が2倍、3倍、4倍になれば、それに応じて
距離であったり水の溜まる量も2倍、3倍、4倍となる。【演習問題】
速さ60[km/h]で走る車が30分ごとに距離[km]を計測します。以下の表を埋めてみよう。
時間[h] 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 距離[km] 0 30 答えは次のブログで!
////////////////////////////////////
「比例を表す式」
のURLを貼り付ける
//////////////////////////////////// -
座標平面とは?
座標平面ってなんだ?という方に向けてのブログです。
座標平面について
座標平面は下の図のような、縦と横の方眼マスに軸を2本引いたことを言います。
座標平面は主に
点をプロットしたり、
直線を引いたり、
曲線を描いたりするときに使われています。ときには三角形や四角形、円などの図形を描く時にも利用されています。
では座標平面について詳しく見ていきましょう。x軸、y軸について
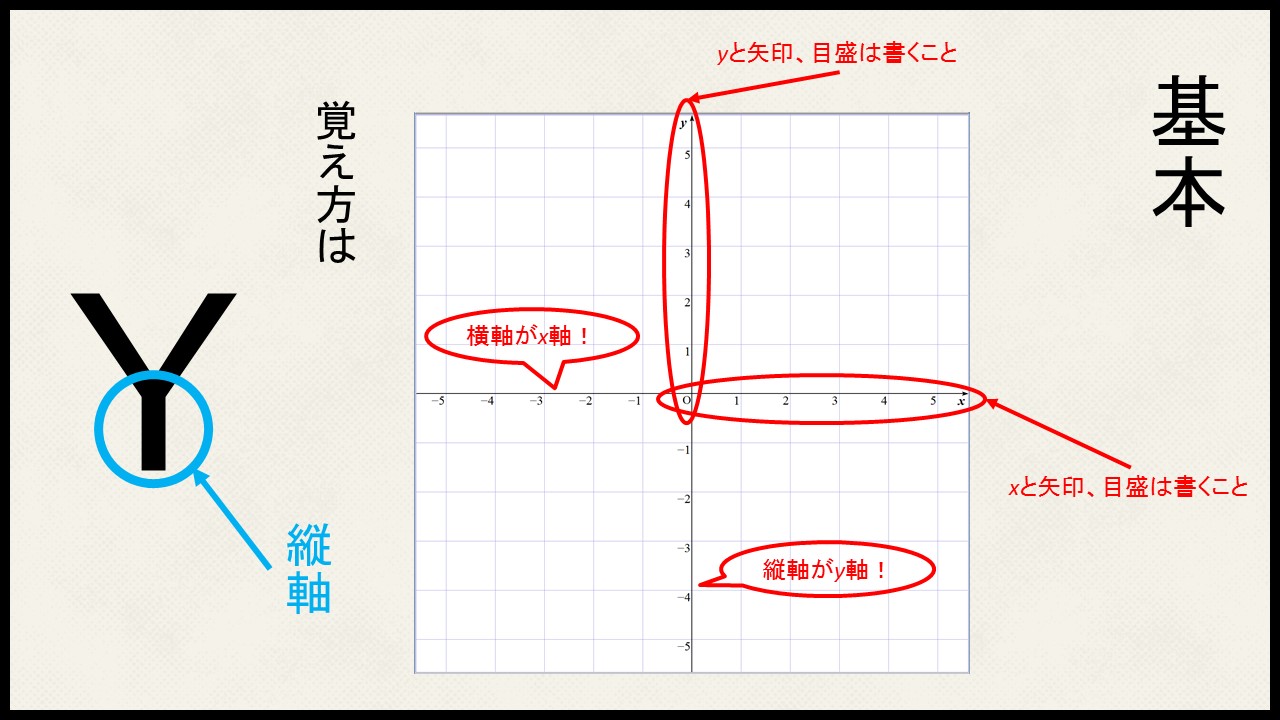
横軸がx軸、縦軸がy軸と名前がついています。
またこのとき、x軸は右に行くと大きくなり、y軸は上に行くと大きくなります。
大きくなる方向に矢印を書き、目盛も入れます。どっちがx軸でどっちがy軸になるかわからなくなったときは下の図を思い出してください!
象限について
座標平面のエリアにはそれぞれ、名称がついています。
x軸とy軸の交点を中心に、右上のエリアから反時計回りに第1象限、第2象限、第3象限、第4象限となっています。

座標について
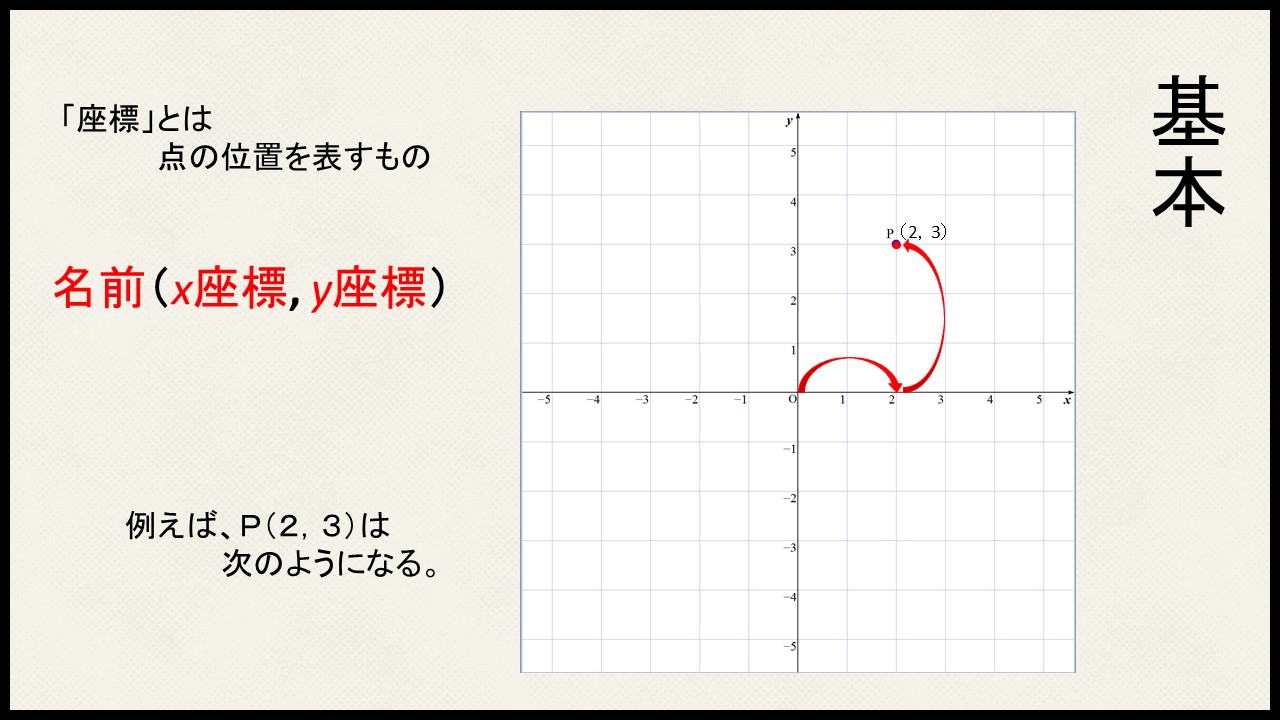
座標とは点の位置を表すものなのでしっかり覚えておきましょう!
どのようにして書かれるかというと、
$$\Large点の名前(x座標,y座標)$$
となっています。
/////////////////////////////////
比例のグラフの
URLを貼る
///////////////////////////////// -
比例のグラフ(その2)
演習問題の解答
//////////////////////////////////////////////////
ここに「比例のグラフ」のURLを貼る
//////////////////////////////////////////////////
比例定数の性質
前回のブログで示したグラフと、上記にある演習の解答のグラフを見比べてみてください。
なにか違いが感じられるのではないでしょうか?
比例定数の正負
比例定数が正の場合、グラフは右肩上がりに伸びます。
(右に行けば行くほど、上にどんどん伸びていきますよね?)逆に比例定数が負の場合は、グラフは右肩下がりに伸びていきます。
(右に行けば行くほど、下にどんどん伸びていきますよね?)比例定数の正負によってグラフの向きが変わります。重要なことなのでしっかり覚えていきましょう。
比例定数の大小
比例定数の絶対値の大小によってグラフはどのようになるでしょうか。
実際に比べてみましょう。
$$y=xとy=2xとy=\frac{1}{2}$$
を実際にグラフに書いてみましょう。
前回のブログではグラフを書くときに点をいっぱい書いたが、
グラフは2点(なるべく離れた点)をプロットすることで書くことができます。ではやってみましょう。
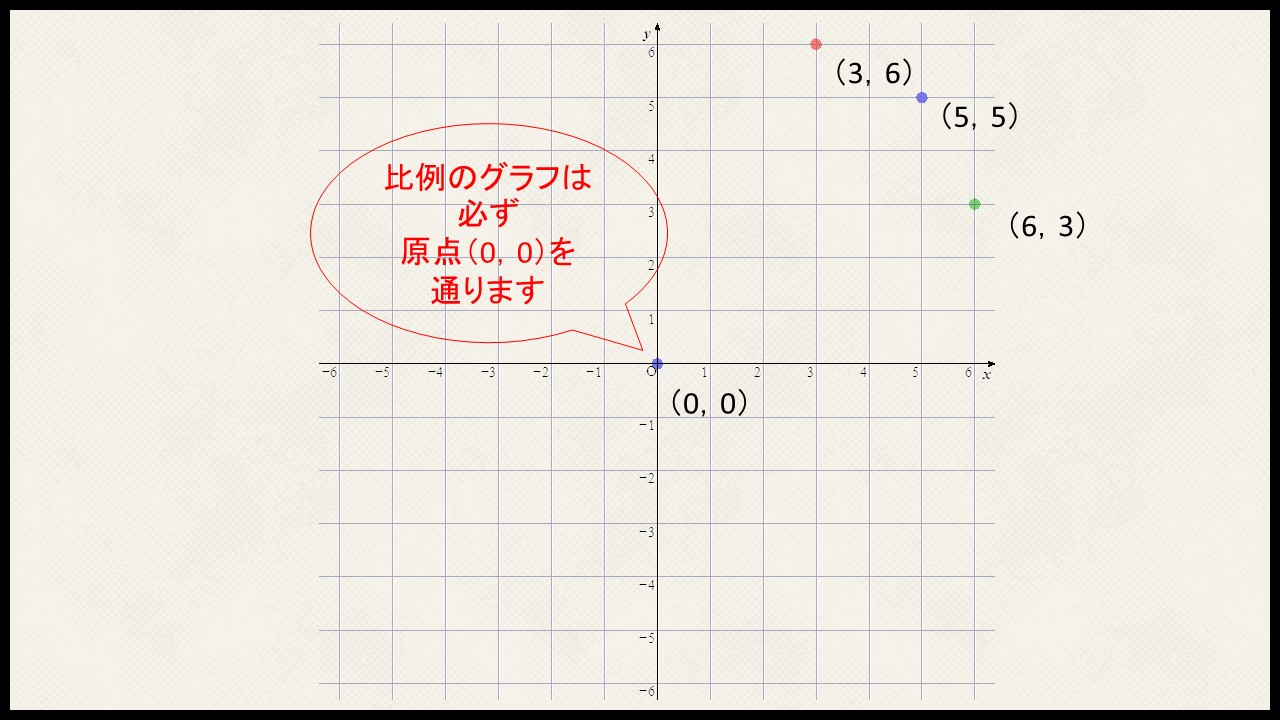
比例のグラフを必ず原点を通ります。x=0を代入するとわかるようにyも0になることがわかるため、比例のグラフは必ず原点を通ることがわかります。
また離れた点を求めプロットし、原点とその点を定規で結べば、グラフを描くことができます。
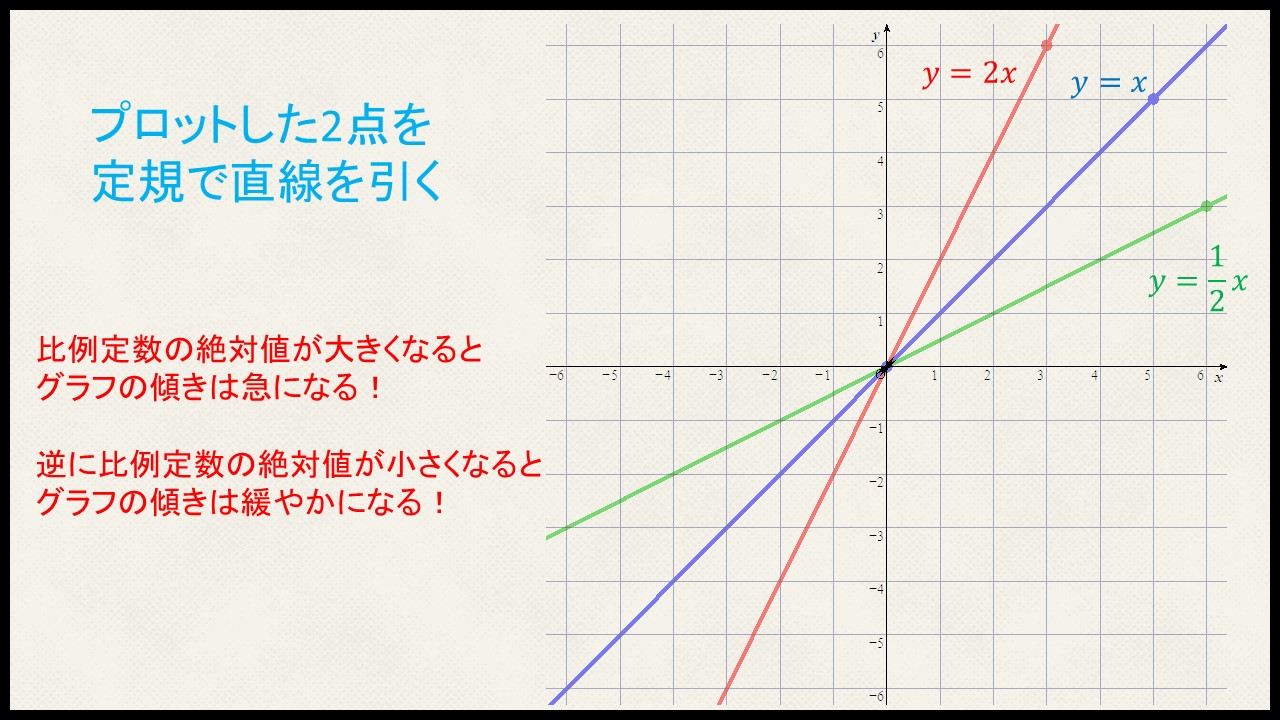
上記のように、赤、青、緑のグラフを見るとわかるように、比例定数の絶対値が大きくなるとグラフの傾きが急になることがわかる。
この関係は非常に大事なため、しっかり覚えておいてください!
グラフから比例定数を求めよう
今までは比例定数からグラフを書いていたが、次はグラフが与えられていて、そのグラフから比例定数を求めるためにはどうすればいいか見ていきましょう。
覚えることはこれだけです!
$$(比例定数)a=\frac{yの増加量}{xの増加量}$$
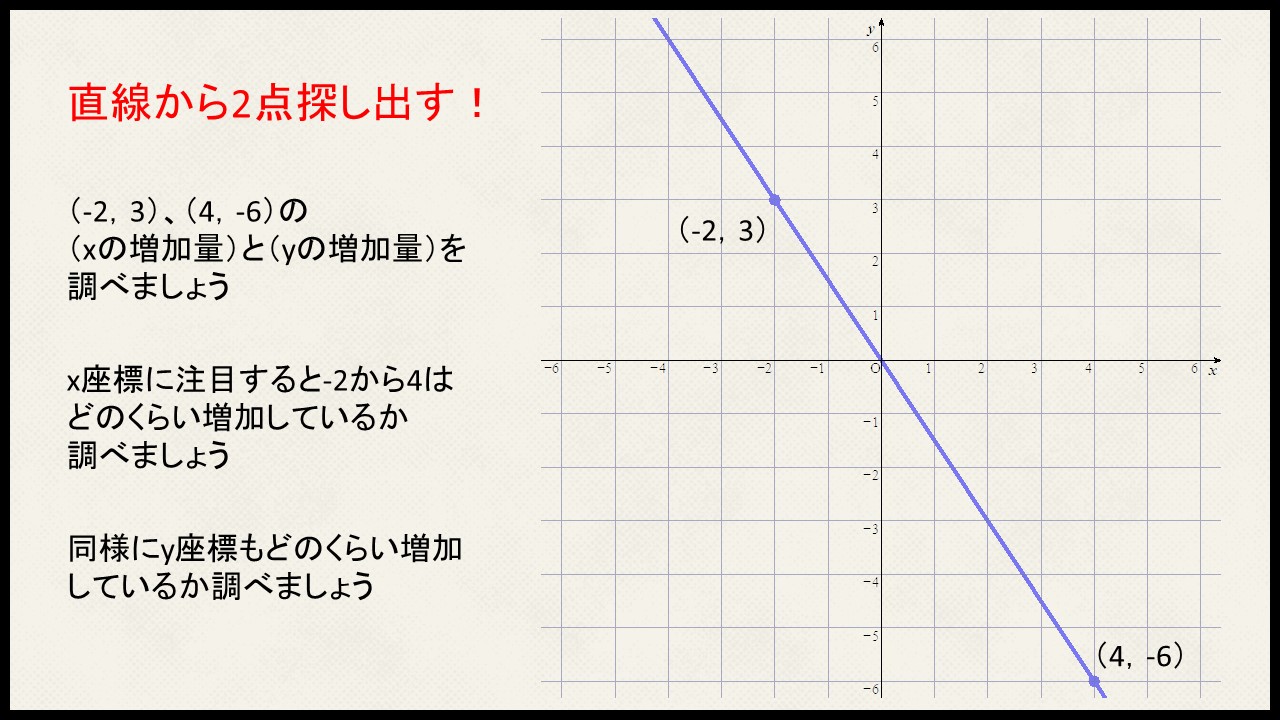
直線から2点を探し出し、それぞれx座標がどのくらい増加したか、y座標がどのくらい増加したか求め、上の公式に当てはめると比例定数は求まります。

比例におけるグラフのポイント
- 比例のグラフは必ず原点を通る!
- 直線の傾きは比例定数を見ると簡単!
$$(比例定数)a=\frac{yの増加量}{xの増加量}$$- 比例定数aがプラスのとき、グラフは右上がりの直線になる。
- 比例定数aがマイナスのとき、グラフは右下がりの直線になる。
- グラフは原点と他の1点を取って直線を引く!
-
比例のグラフ
前回(比例を表す式)解答
//////////////////////////////////////////////////
ここに「比例を表す式」のURLを貼る
//////////////////////////////////////////////////(1)
$$y=2\times3x=6x$$
よってyはxに比例し、比例定数は6となる。(2)
$$y=100\times x=100x$$
よってyはxに比例し、比例定数は100となる。(3)
$$y=ax$$
に代入すると
$$\begin{eqnarray*}
15&=&a\times10\\
a&=&\frac{15}{10}\\
a&=&\frac{3}{2}
\end{eqnarray*}$$
より比例定数は求まった。比例の式は以下のとおりである。
$$y=\frac{3}{2}x$$
となる。またx=4のとき、yの値は
$$\begin{eqnarray*}
y&=&\frac{3}{2}\times4\\
y&=&\frac{3\times4}{2}\\
y&=&6
\end{eqnarray*}$$
よりy=6となった。y=9のとき、xの値は
$$\begin{eqnarray*}
9&=&\frac{3}{2}x\\
x&=&9\times\frac{2}{3}\\
x&=&\frac{9\times2}{3}\\
x&=&6
\end{eqnarray*}$$
よりx=6となった。(4)
$$y=x\times x=x^{2}$$
よってyはx2に比例し、yはxに比例していない。(5)
$$y=24-x$$
よってyはxに比例していない。(y=axの関係が成り立っていないため)比例の式をグラフに
ではこれから比例の式を座標平面上に表してみましょう!
「座標平面って何?」という方は下のブログで!
////////////////////////////////////////////
「座標平面について」の
URLをここに貼る
/////////////////////////////////////////////では前回の演習問題(3)の問題を用いて表とグラフを書きましょう。
比例の式は
$$y=\frac{3}{2}x$$
であるので、下の表を完成させましょう。
x座標 -4 -3 -2 -1 0 1 2 3 4 y座標 x座標 -4 -3 -2 -1 0 1 2 3 4 y座標 -6 $$-\frac{9}{2}$$ -3 $$-\frac{3}{2}$$ 0 $$\frac{3}{2}$$ 3 $$\frac{9}{2}$$ 6 では上記の表を座標平面上にプロットしましょう。
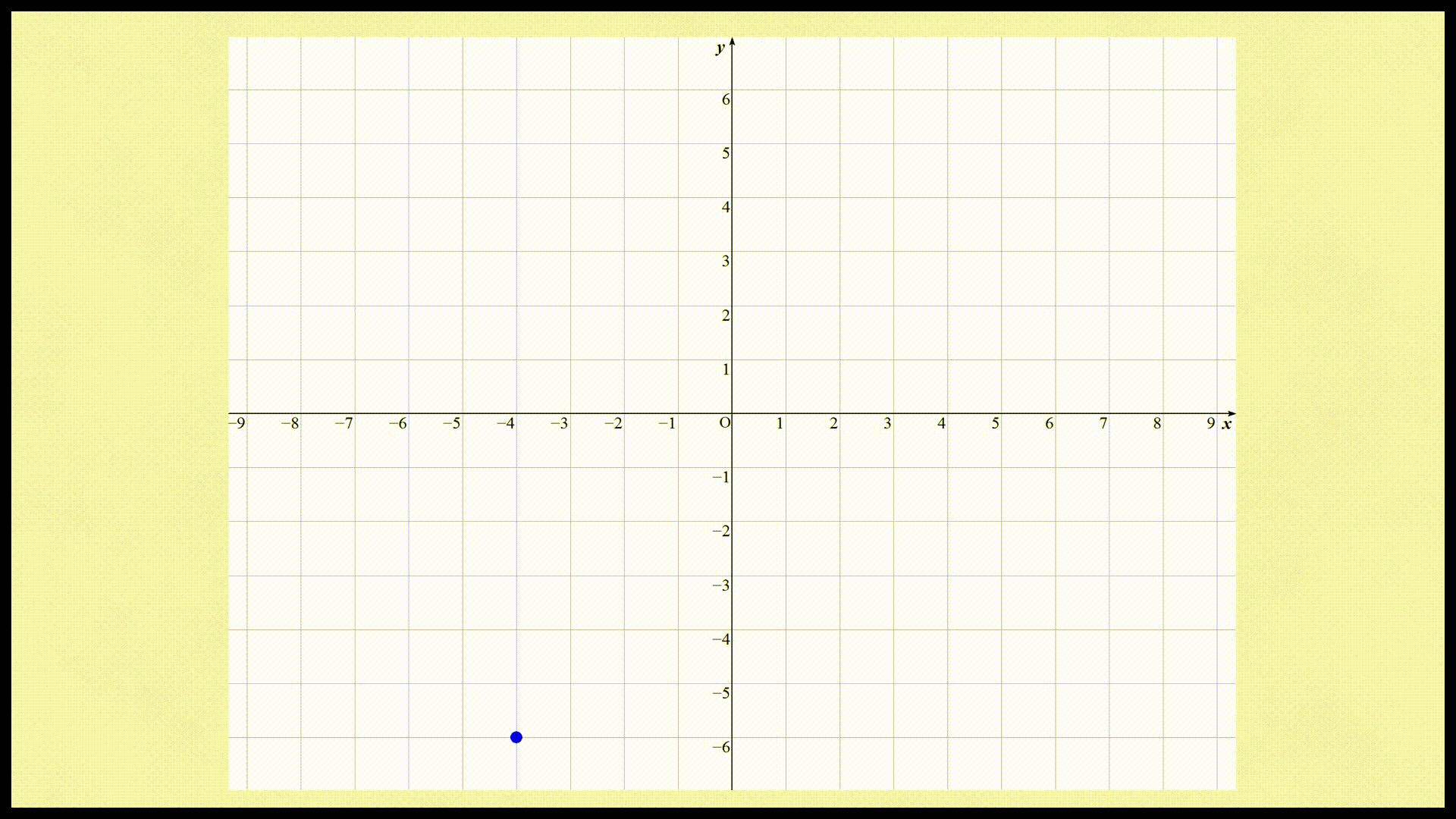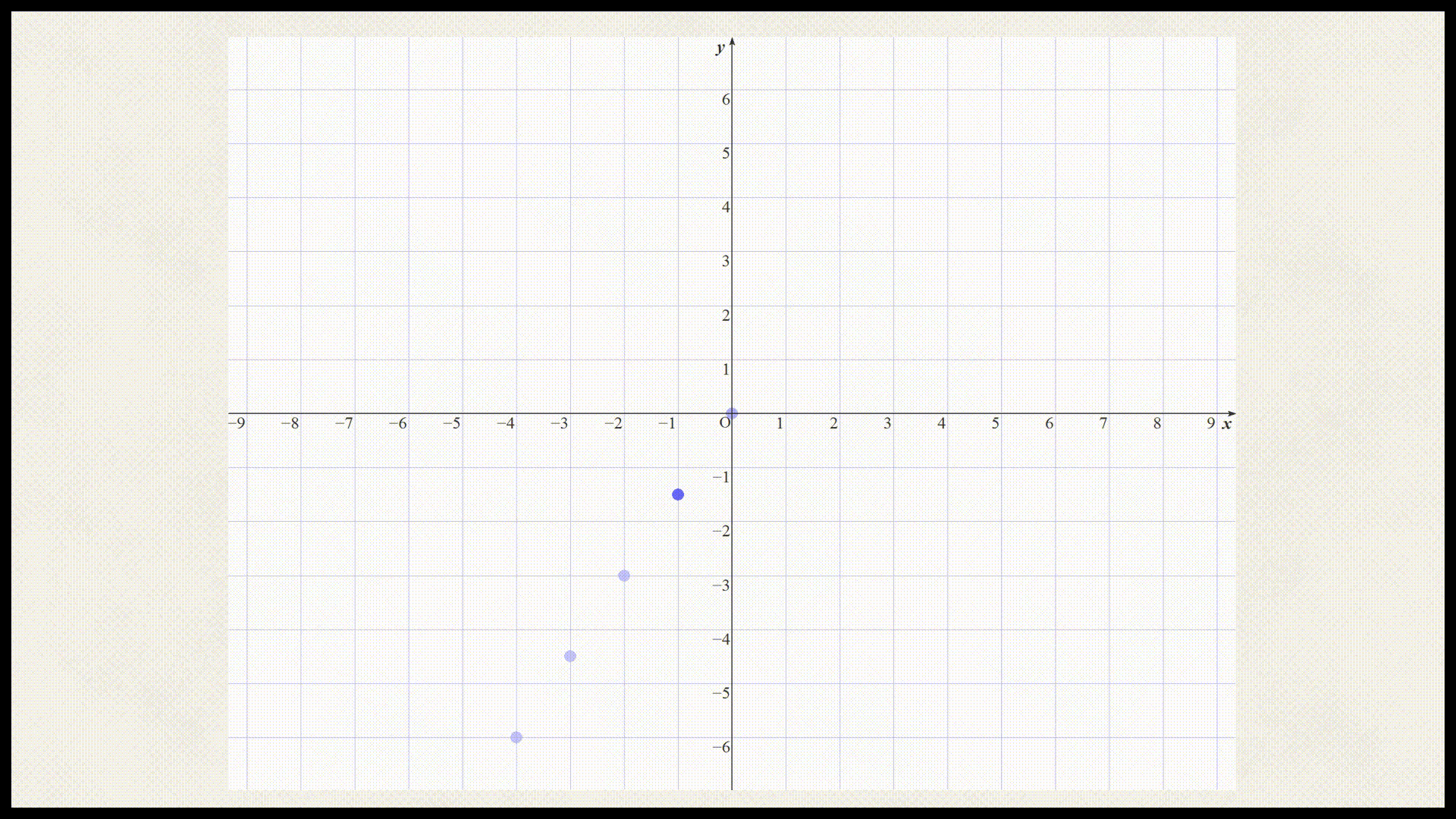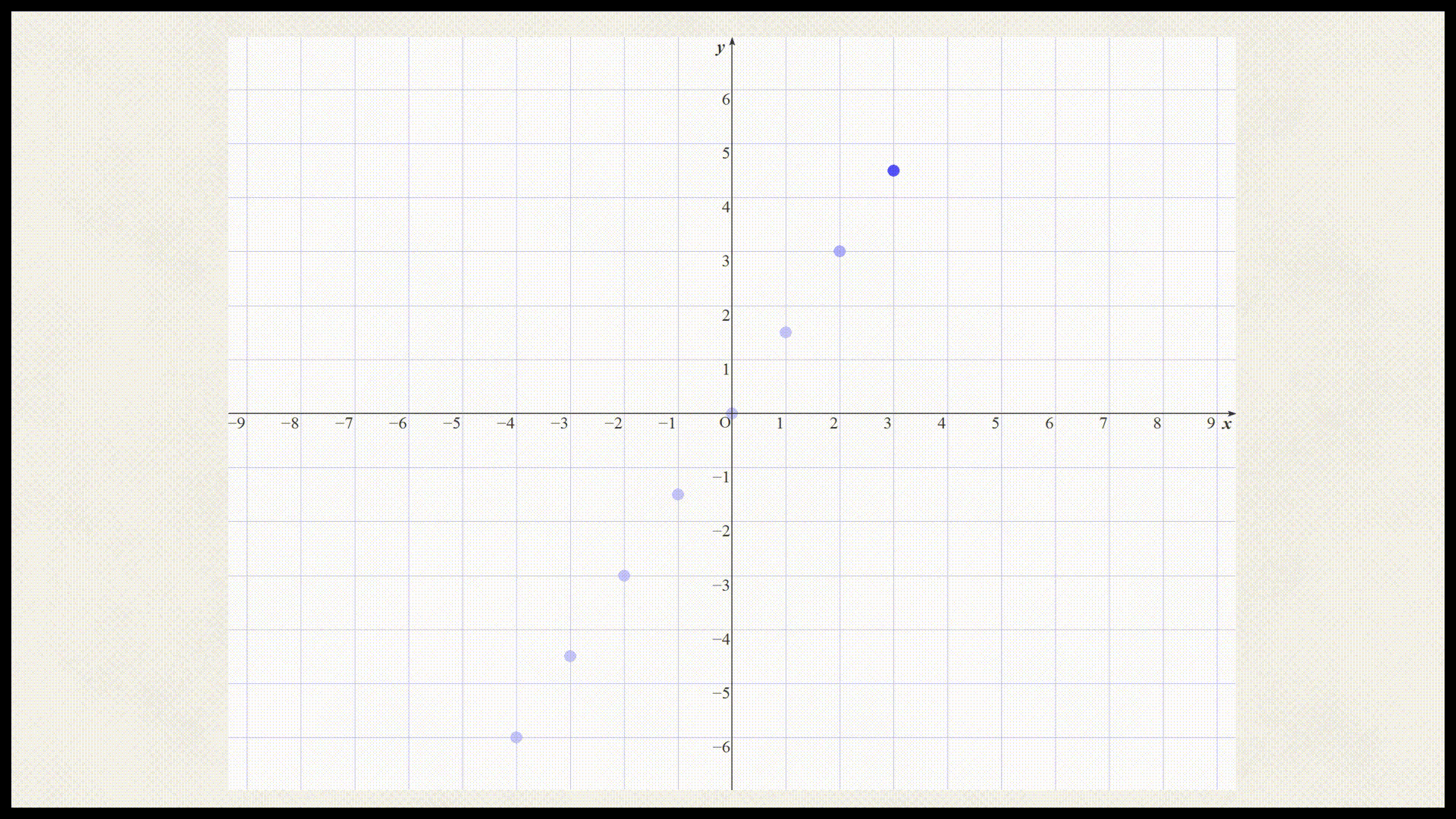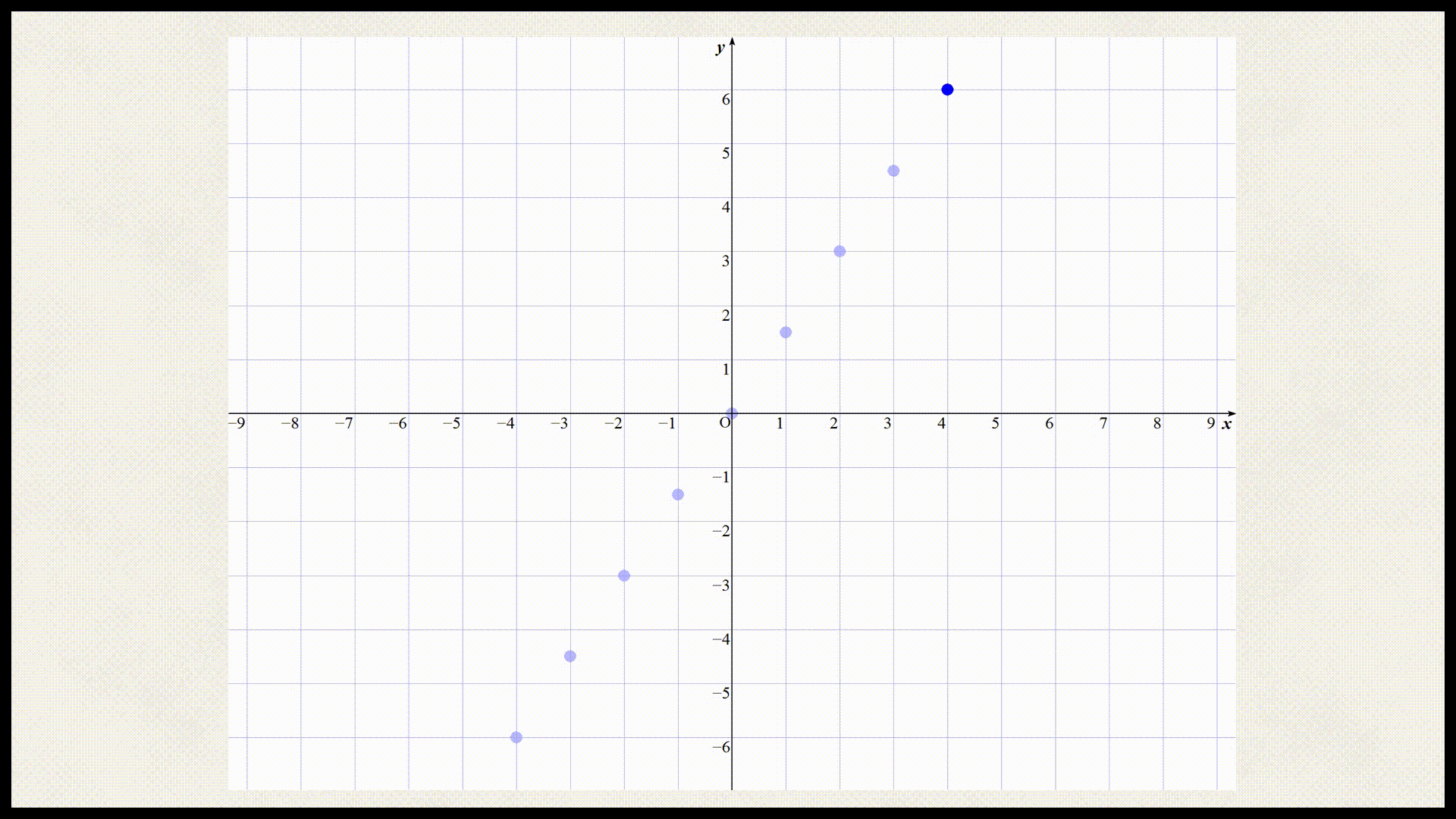
これらの点を直線で結ぶと以下のようになる。
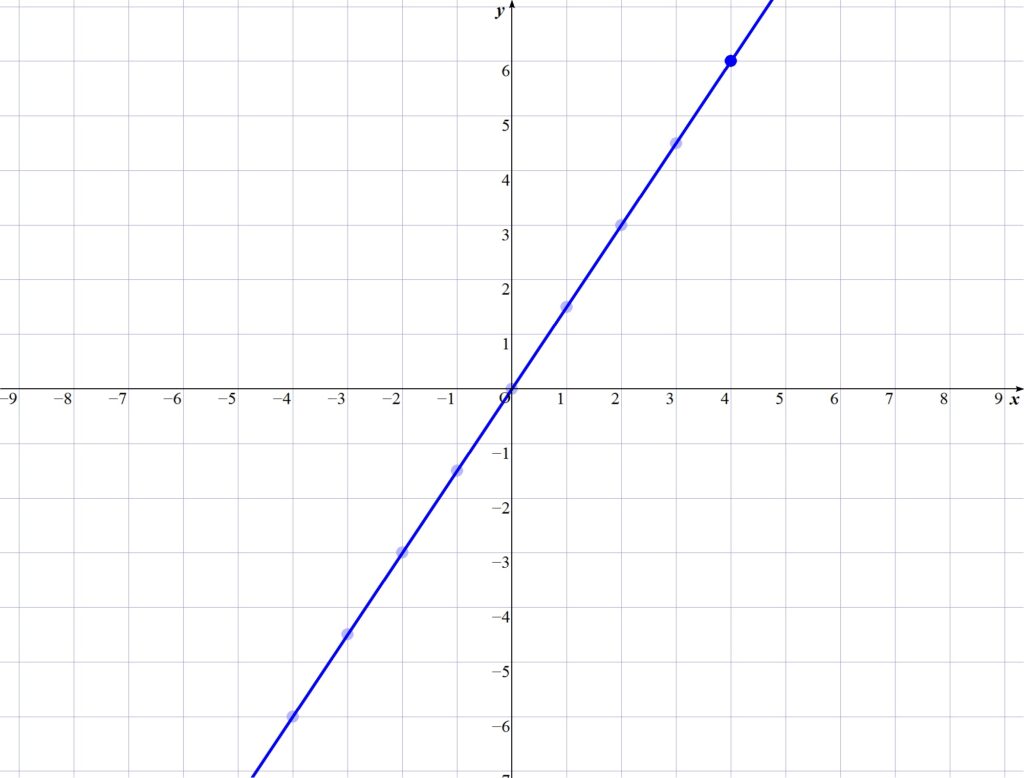
上記が比例におけるグラフになります。
ではグラフの書き方が分かったと思いますので、演習問題をやってみましょう。
次回は比例のグラフをもっと詳しく見ていきます。
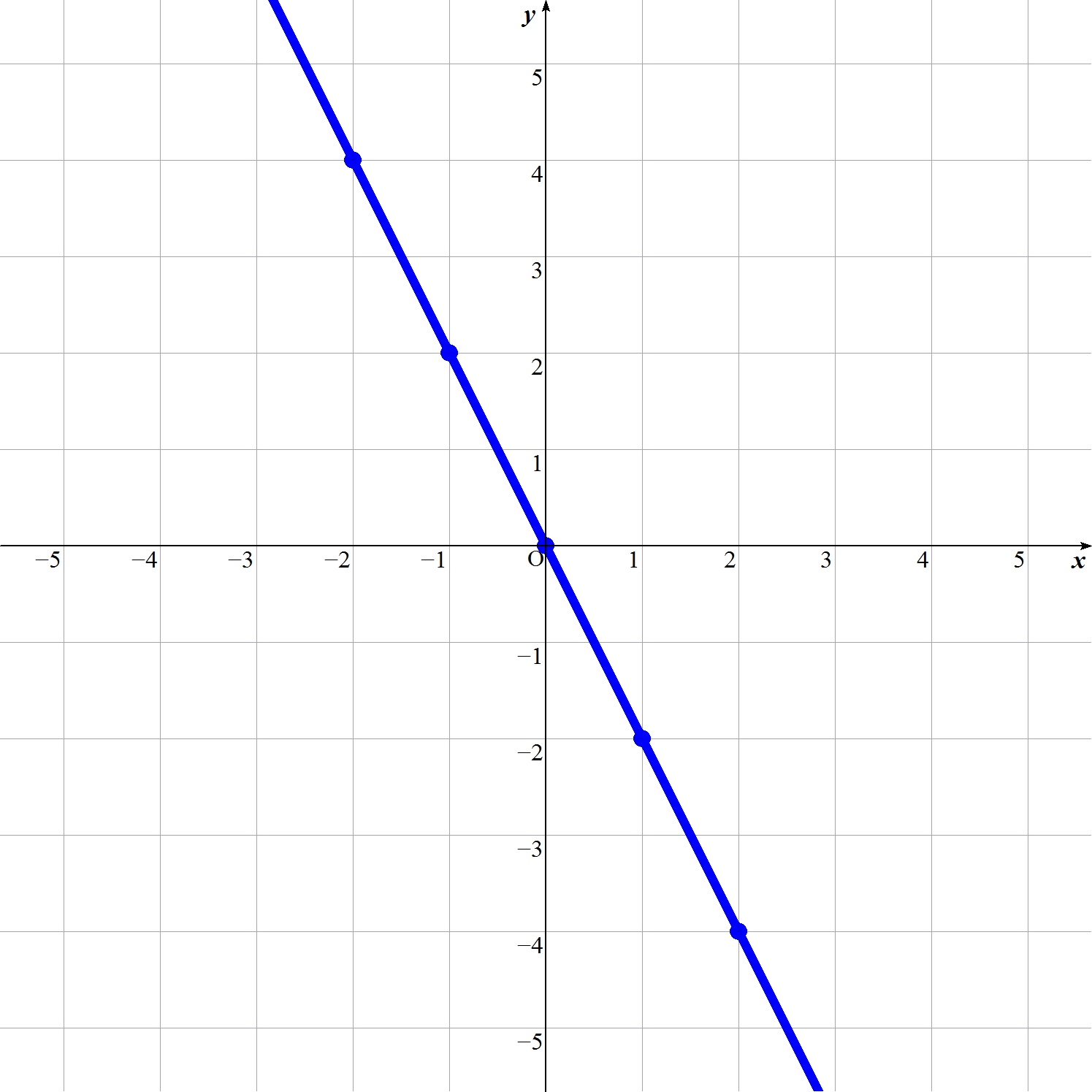
演習問題
$$y=-2x$$
のグラフを描いてください。
解答は次のブログで!
//////////////////////////////////////////////////
ここに「比例のグラフ(その2)」のURLを貼る
////////////////////////////////////////////////// -
比例を表す式
前回(比例とは?)の解答
//////////////////////////////////////////////////
ここに「比例とは」のURLを貼る
//////////////////////////////////////////////////時間[h] 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 距離[km] 0 30 60 90 120 150 180 210 240 比例を式に!
では「比例とは」のブログで示した日常生活における例を式にし、グラフ化していきます。
なぜわざわざ式やグラフで表さなくてはならないのか。
これは時間を代入すると水の深さや移動した距離を簡単に求めることができ、とても簡単に結果を知ることができます。
また、グラフを書くことで時間と距離や長さの関係を視覚化し、よりわかりやすくすることができます。
比例の式 y=ax
まずは比例の式を覚えましょう。
$$y=ax$$
ではそれぞれの役割について見ていきましょう。
xは前記の具体例では時間を表します。
yは水の深さや移動した距離を表します。
aは「比例定数」と呼ばれ、歩く速度や水を入れる量を表します。
そしてxとyの関係がy=axとなるとき「yはxに比例する」と言います。
ここで注意する点として比例定数aはゼロにはならないことです。
例題
次の(1)~(3)についてyがxに比例するかどうか調べましょう。また比例するものについては、比例定数を求めなさい。
(1)1辺3x[cm]の正方形の面積をy[cm2]とする。
(2)1個300円のショートケーキをx個買う時の代金をy円とする。
(3)1000mの距離を秒速x[m]で走ったときにかかる時間をy秒とする。解答
(1)
$$y=3x\times3x=9x^2$$
よってyはx2に比例し、yはxに比例していない。(2)
$$y=300\times x=300x$$
よってyはxに比例し、比例定数は300となる。(3)
$$y=1000\div x=\frac{1000}{x}$$
よってyはxに比例しない。【演習問題】
次の問で、yがxに比例するかどうか調べましょう。また比例するものについては、比例定数を求めなさい。(3)は比例の式、比例定数とそれぞれの問に答えよ。
(1)半径3x[cm]の円の周の長さy[cm]
(2)分速100[m]でx分歩いた時の距離y[m]
(3)x=10の時、y=15である。
x=4のときのyの値を求めよ。
y=9のときのxの値を求めよ。(4)長さx[cm]の正方形の面積y[cm2]
(5)一日の夜の長さx時間の時、朝と昼の長さy時間。
-
数学で必ずやっておきたい復習チェックポイント&復習法
勉強と言っても「予習」「復習」「問題演習」などありますよね。さて、この中でもどれを一番重視するべきでしょうか?
それは、「復習」です。
もちろん、授業をサラッと理解するための「予習」、解答力を付けるための「問題演習」も大事です。しかし、何よりも重要なのは「復習」です。なぜ復習がそんなに重要か、また、復習と言っても、実際どうやってやればいいの?という疑問にお答えしていこうと思います。
-

最短最速で中学英単語を覚える3つの方法
英語を勉強するときに、一番最初にやることは「単語を覚えること」でしょう。
「暗記って苦手なんだよね」と思っているとしたら、それは幻想です。単語暗記は「作業」です。頭の善し悪しは全く関係ありません。
数をこなすことが求められる勉強です。勉強だ!と意気込む必要も特にないような気もします。
まずはさっさと単語を覚えてしまって、今後の英語学習をスムーズに進められるようにしちゃいましょう。
-
ひらめきに頼らず中学数学の図形問題を解く7つのコツ
数学の中で特に苦手な人が多いのが図形問題だと思います。「図形ってひらめきが全てじゃないの?」と思っている人が沢山いる気がします。
しかし、実は図形問題も工夫次第で全くひらめきに頼ることなく問題を解いていくことができます。図形問題でも、他の計算問題と同じで「やること」や「やることの順序」が決まっているのです。
ひらめきで解いてるいるように見える人も(一部を除いて)、実は解くときに決まったことを決まった順序で素早くやっているだけなのです。
-

【数学】中学証明問題を解く4つのポイント
今回は中学数学のヤマ。証明問題の解き方についてコツを紹介していきます。証明問題のコツ4ポイントについて説明します。
次の問題を例に4ポイントを確認してみましょう。

1.図形の性質や条件をとにかく覚える
- 三角形の合同条件
- 三角形の相似条件
- 平行線の性質
- 平行四辺形になる条件
- 直角三角形の合同条件
- 二等辺三角形の性質
など
これが何よりも大事といっても過言ではありません。
証明問題において、図形の性質や条件が決め手となります。
しかし、それらは実際のテスト本番で思いつくことができないので、覚えていなければ致命的になってしまいます。(ほとんど点数は来ないと思ってください。)
なので、とにかく図形の性質・条件を覚えてお経のように唱えられるようになる!!これに尽きます。
【この例題では】
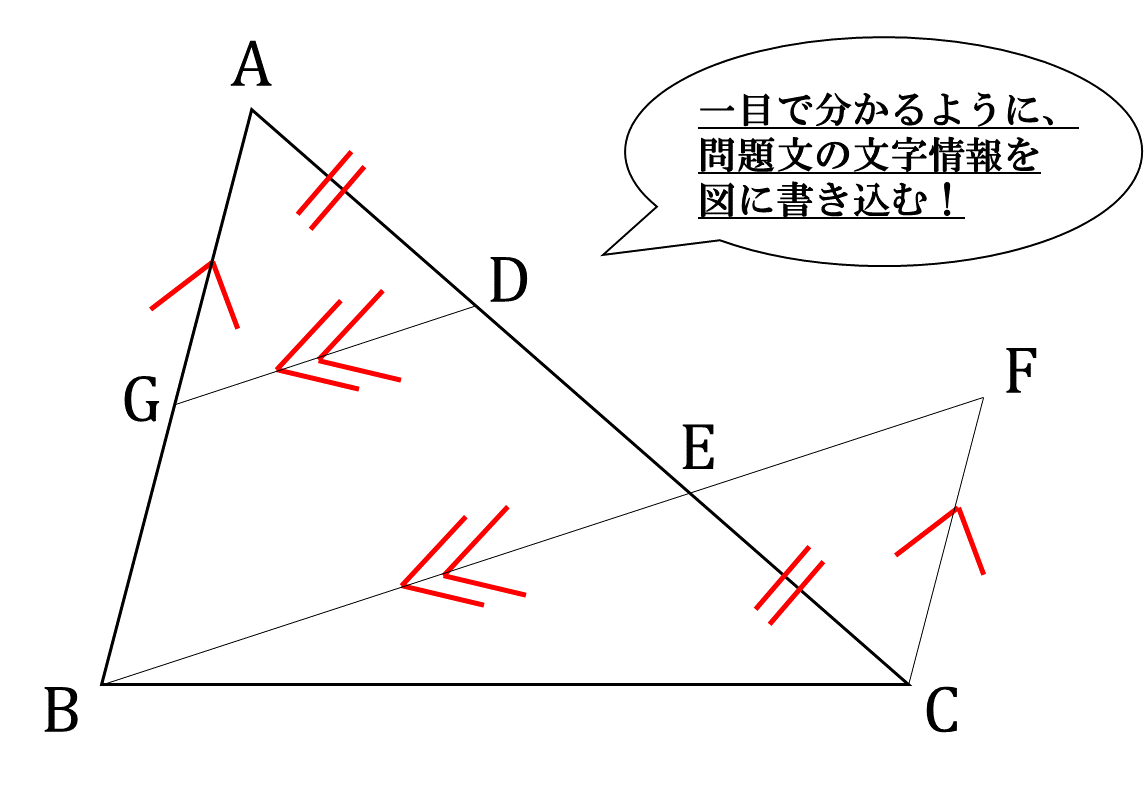
まず、「AB∥CF」「GD∥BF」と書いてあるので、平行線の性質が使えそうです。
平行線の性質としては「①同位角が等しい」「②錯角が等しい」がありましたね。
2.「仮定」と「結論」を探してチェック、「条件」は図に書き込む
ここでの「仮定」は「AD=CE」「AB∥CF」「GD∥BF」です。「仮定」は出題者が一方的に決めている条件で、図だけからは分からないので、しっかりと確認しましょう。
またここでの「結論」は「△AGD≡△CFEを証明する」です。数学の問題全般に言えることですが、「結論=求めたいもの」は求める過程で大きなヒントとなることが多いです。なので忘れることなく、常に意識しておく必要があります。
条件はどんどん図に書きこんで(下図の赤線のように)、一目で分かるようにすることが大切です。
3.結論を見て、覚えた図形の条件のどれを使うか決める
図形の条件とは「三角形の合同条件」「三角形の相似条件」のことです。
問題文の仮定、結論、図をじっくりみてどの条件を使うか考えましょう。
【この例題では】
2でも書いた通り、結論は「△AGD≡△CFE」、仮定は「AD=CE」「AB∥CF」「GD∥BF」ですよね。
まず合同を証明するので、
①3辺がそれぞれ等しい
②2辺とその間の角がそれぞれ等しい
③1辺とその両端の角がそれぞれ等しい
の三つのどれかとなります。
次に仮定を見ると、「AD=CE」「AB∥CF」「GD∥BF」で、
1でも書いたように、平行線の性質から「同位角や錯角が等しいこと」が分かるから、
「角」の条件を使うという予測が立ちます。
そして上の3つの合同条件と見比べて、「③1辺とその両端の角がそれぞれ等しい」を使おう、と決まります。
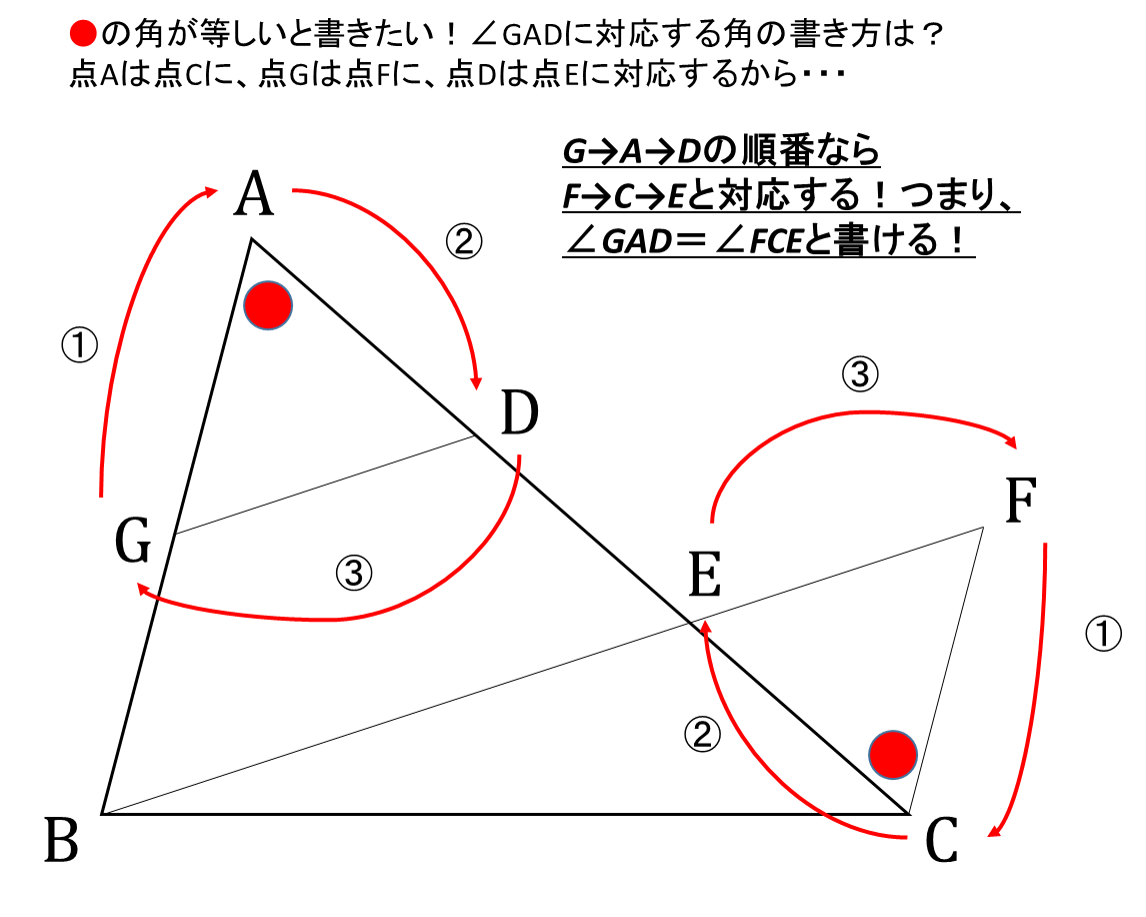
4.アルファベットが対応しているか確認する
ここでは「∠GAD=∠FCE(錯角)」の条件を使いますが、このアルファベットの並び方は証明する図形の点の並び方と一致していなければなりません。
「△AGD≡△CFE」を示すので、点Aは点Cに、点Gは点Fに、点Dは点Eに対応します。
「∠GAD=∠ECF」は数学的な意味では「∠GAD=∠FCE」と同じですが、証明の記述としては間違いとなるので注意しましょう。