カテゴリー: 未分類

座標平面ってなんだ？という方に向けてのブログです。

座標平面について

座標平面は下の図のような、縦と横の方眼マスに軸を2本引いたことを言います。

座標平面は主に
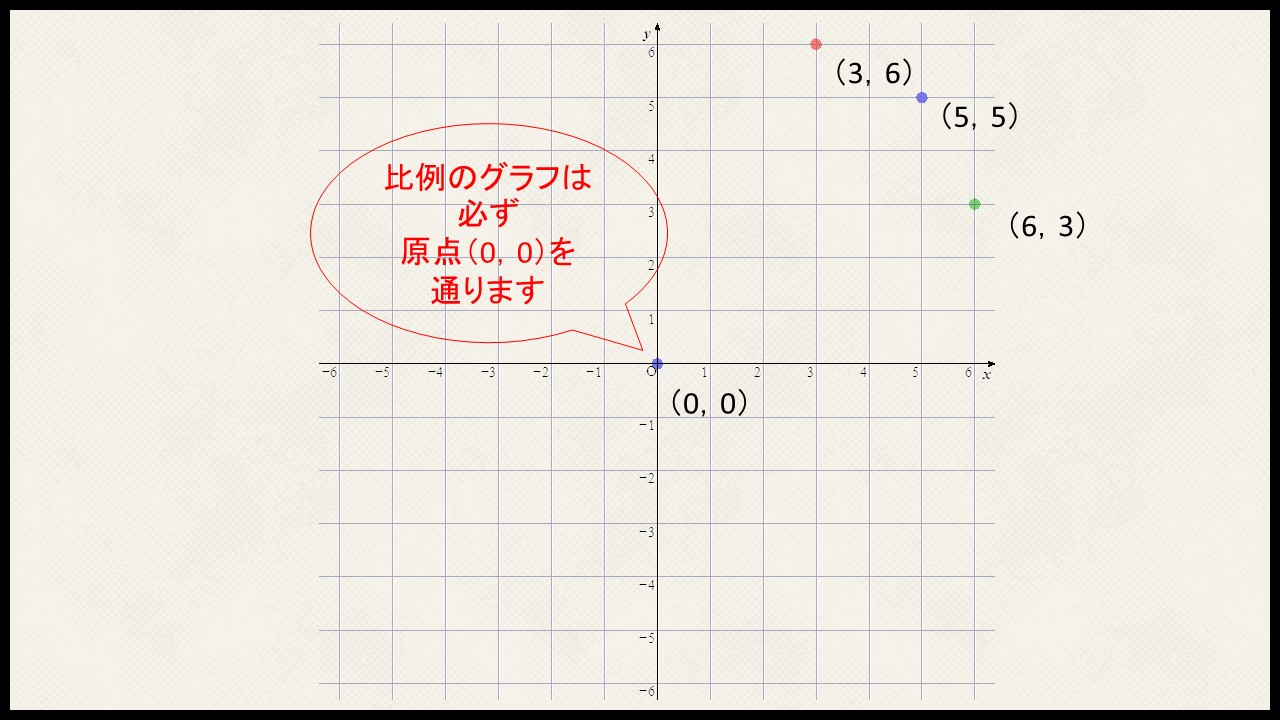
点をプロットしたり、
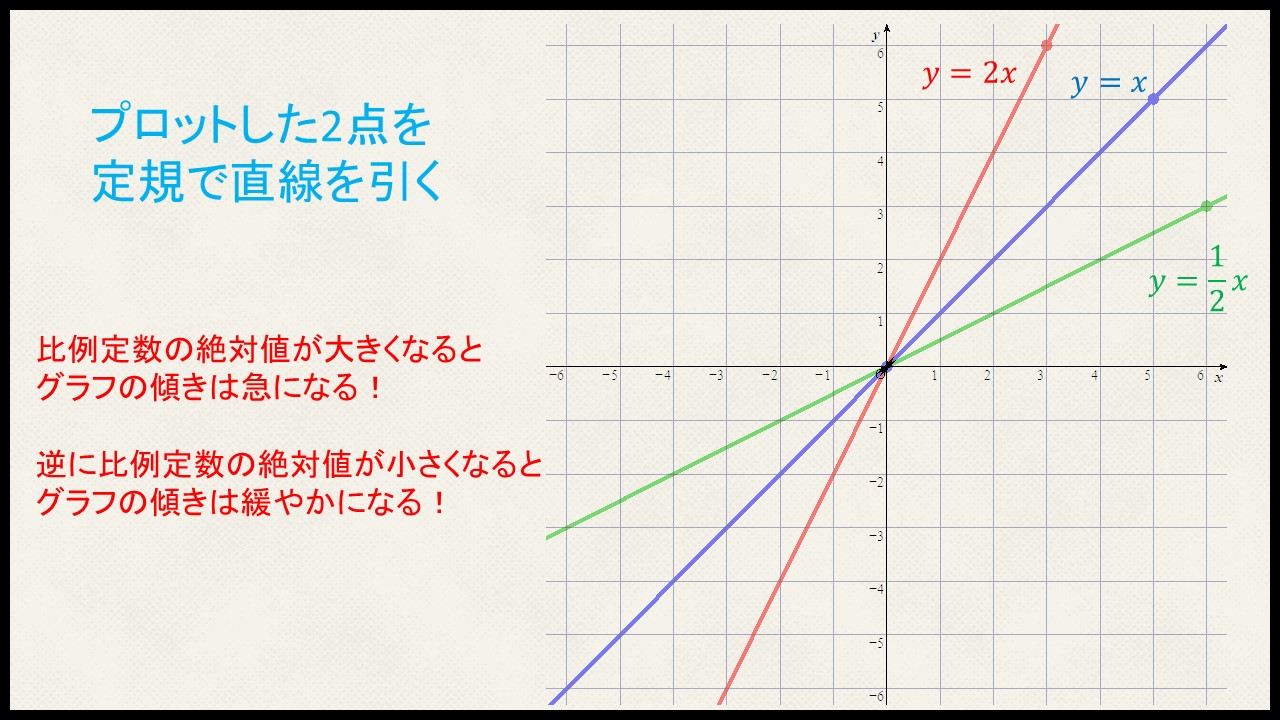
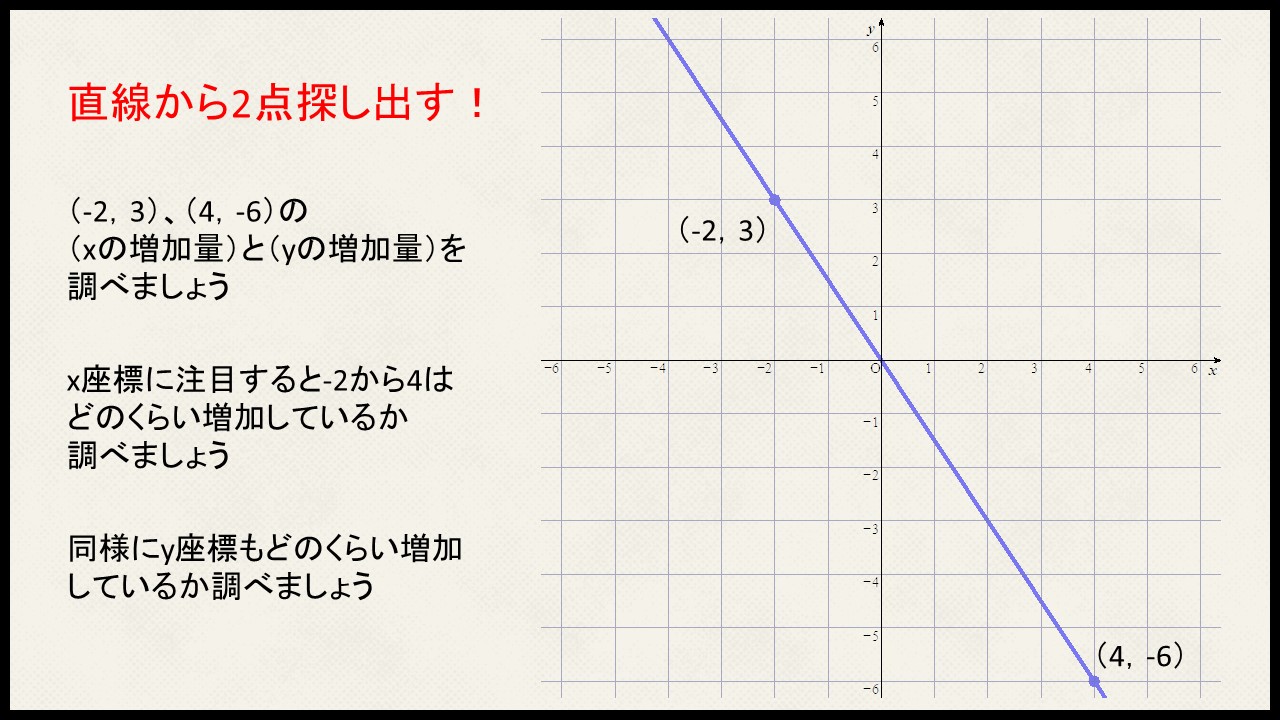
直線を引いたり、
曲線を描いたりするときに使われています。

ときには三角形や四角形、円などの図形を描く時にも利用されています。
では座標平面について詳しく見ていきましょう。

x軸、y軸について

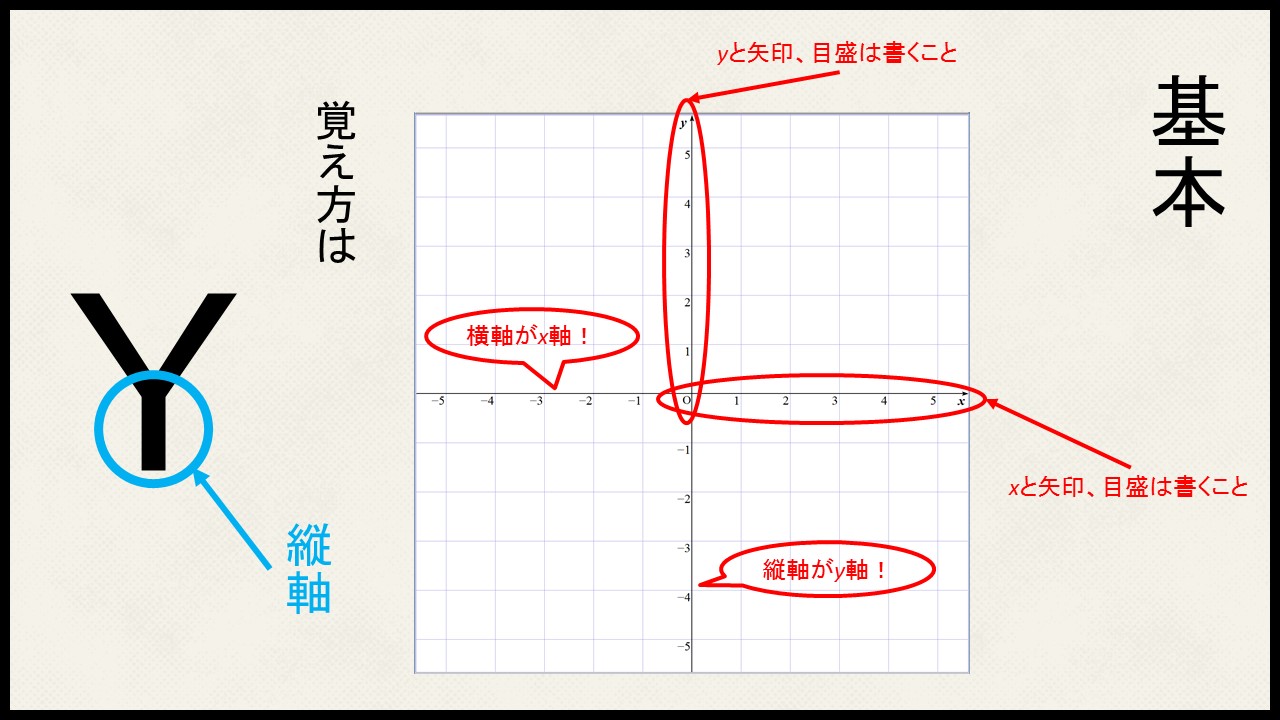
横軸がx軸、縦軸がy軸と名前がついています。
またこのとき、x軸は右に行くと大きくなり、y軸は上に行くと大きくなります。
大きくなる方向に矢印を書き、目盛も入れます。

どっちがx軸でどっちがy軸になるかわからなくなったときは下の図を思い出してください！

 

象限について

座標平面のエリアにはそれぞれ、名称がついています。

x軸とy軸の交点を中心に、右上のエリアから反時計回りに第1象限、第2象限、第3象限、第4象限となっています。

 

座標について

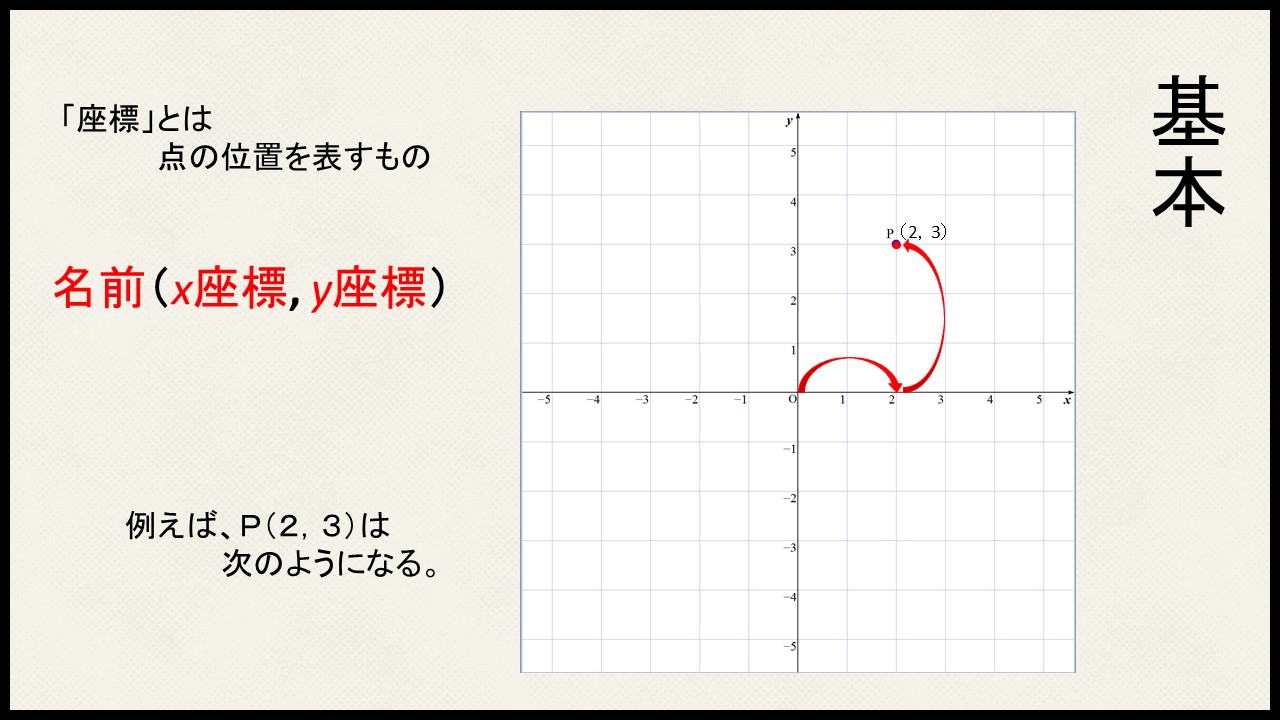
座標とは点の位置を表すものなのでしっかり覚えておきましょう！

どのようにして書かれるかというと、

$$\Large点の名前（x座標，y座標）$$

となっています。

 

/////////////////////////////////
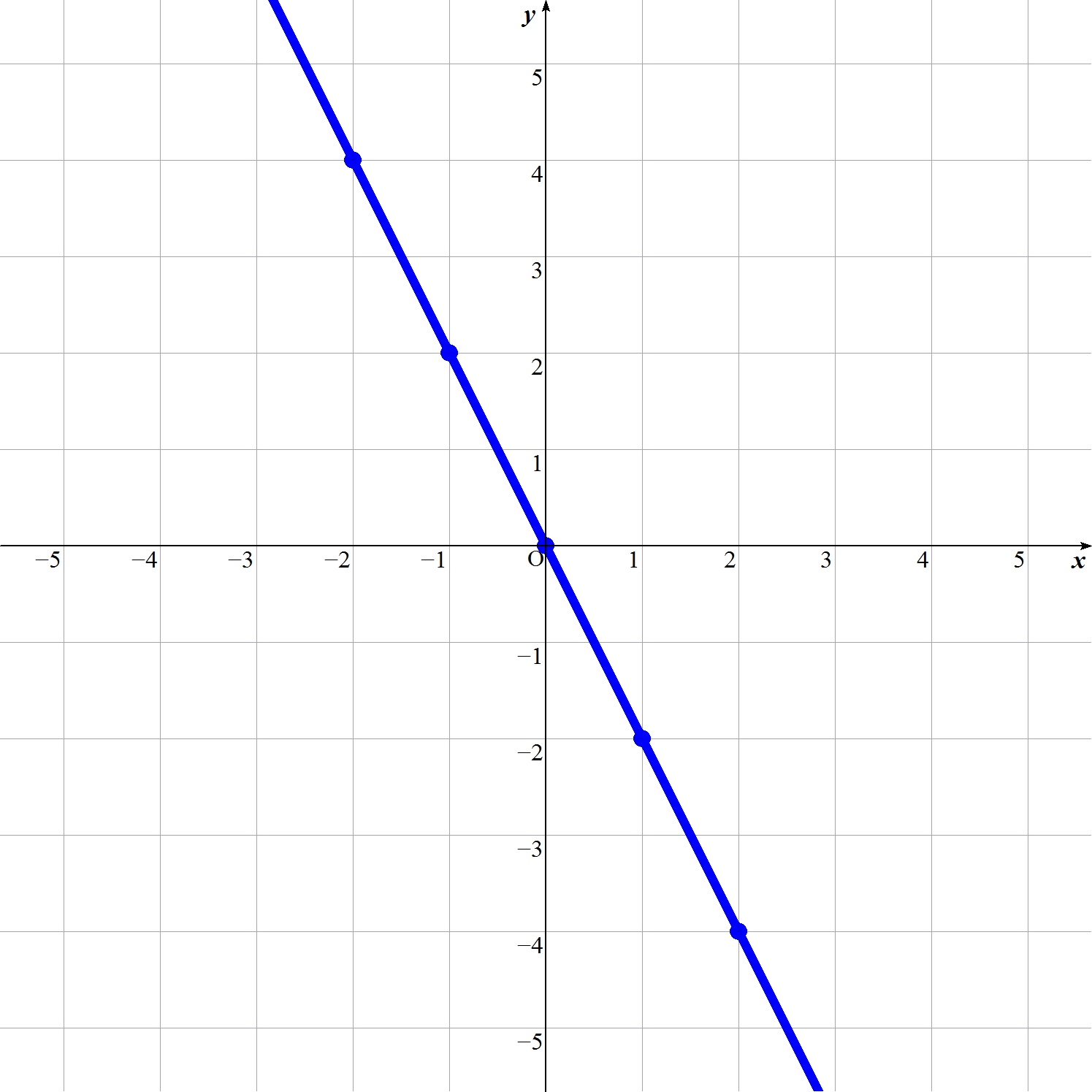
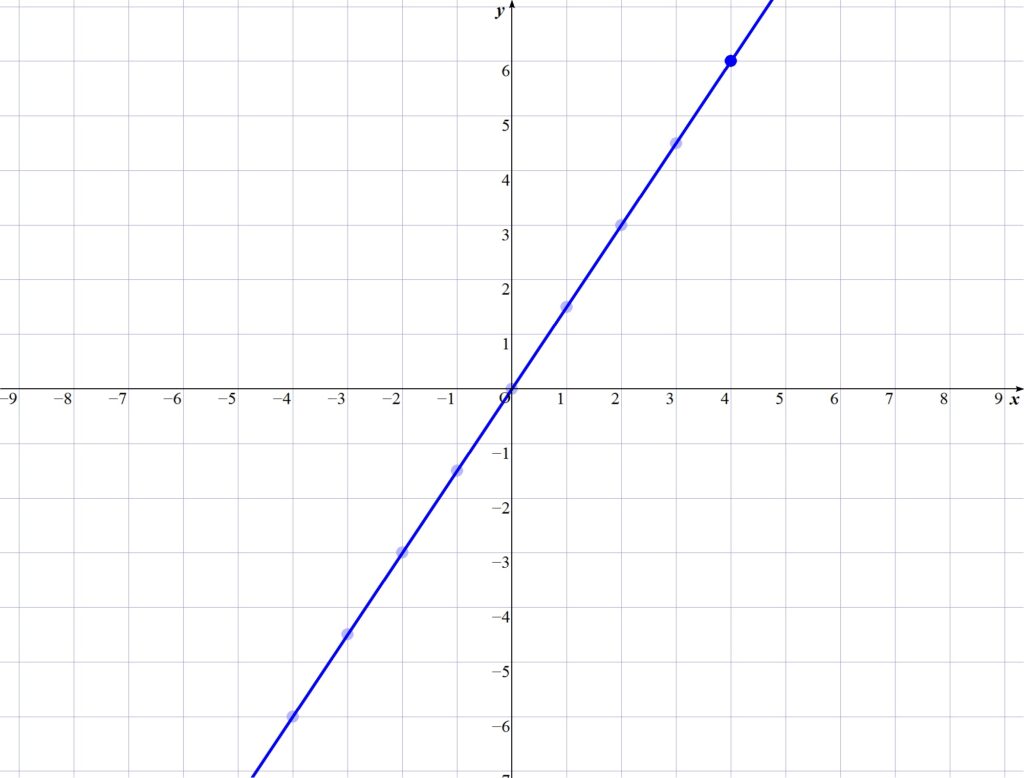
比例のグラフの
URLを貼る
/////////////////////////////////

演習問題の解答

//////////////////////////////////////////////////
ここに「比例のグラフ」のURLを貼る
//////////////////////////////////////////////////

比例定数の性質

前回のブログで示したグラフと、上記にある演習の解答のグラフを見比べてみてください。

なにか違いが感じられるのではないでしょうか？

比例定数の正負

比例定数が正の場合、グラフは右肩上がりに伸びます。
（右に行けば行くほど、上にどんどん伸びていきますよね？）

逆に比例定数が負の場合は、グラフは右肩下がりに伸びていきます。
（右に行けば行くほど、下にどんどん伸びていきますよね？）

比例定数の正負によってグラフの向きが変わります。重要なことなのでしっかり覚えていきましょう。

比例定数の大小

比例定数の絶対値の大小によってグラフはどのようになるでしょうか。

実際に比べてみましょう。

$$y=xとy=2xとy=\frac{1}{2}$$

を実際にグラフに書いてみましょう。

前回のブログではグラフを書くときに点をいっぱい書いたが、
グラフは2点（なるべく離れた点）をプロットすることで書くことができます。

ではやってみましょう。

比例のグラフを必ず原点を通ります。x=0を代入するとわかるようにyも0になることがわかるため、比例のグラフは必ず原点を通ることがわかります。

また離れた点を求めプロットし、原点とその点を定規で結べば、グラフを描くことができます。

上記のように、赤、青、緑のグラフを見るとわかるように、比例定数の絶対値が大きくなるとグラフの傾きが急になることがわかる。

この関係は非常に大事なため、しっかり覚えておいてください！

 

グラフから比例定数を求めよう

今までは比例定数からグラフを書いていたが、次はグラフが与えられていて、そのグラフから比例定数を求めるためにはどうすればいいか見ていきましょう。

覚えることはこれだけです！

$$(比例定数)a=\frac{yの増加量}{xの増加量}$$

直線から2点を探し出し、それぞれx座標がどのくらい増加したか、y座標がどのくらい増加したか求め、上の公式に当てはめると比例定数は求まります。

比例におけるグラフのポイント

1. 比例のグラフは必ず原点を通る！
2. 直線の傾きは比例定数を見ると簡単！
   $$(比例定数)a=\frac{yの増加量}{xの増加量}$$
   1. 比例定数aがプラスのとき、グラフは右上がりの直線になる。
   2. 比例定数aがマイナスのとき、グラフは右下がりの直線になる。
3. グラフは原点と他の1点を取って直線を引く！

前回（比例を表す式）解答

//////////////////////////////////////////////////
ここに「比例を表す式」のURLを貼る
//////////////////////////////////////////////////

（１）
$$y=2\times3x=6x$$
よってyはxに比例し、比例定数は6となる。

（２）
$$y=100\times x=100x$$
よってyはxに比例し、比例定数は100となる。

（３）
$$y=ax$$
に代入すると
$$\begin{eqnarray*}
15&=&a\times10\\
a&=&\frac{15}{10}\\
a&=&\frac{3}{2}
\end{eqnarray*}$$
より比例定数は求まった。比例の式は以下のとおりである。
$$y=\frac{3}{2}x$$
となる。またx=4のとき、yの値は
$$\begin{eqnarray*}
y&=&\frac{3}{2}\times4\\
y&=&\frac{3\times4}{2}\\
y&=&6
\end{eqnarray*}$$
よりy=6となった。y=9のとき、xの値は
$$\begin{eqnarray*}
9&=&\frac{3}{2}x\\
x&=&9\times\frac{2}{3}\\
x&=&\frac{9\times2}{3}\\
x&=&6
\end{eqnarray*}$$
よりx=6となった。

（４）
$$y=x\times x=x^{2}$$
よってyはx²に比例し、yはxに比例していない。

（５）
$$y=24-x$$
よってyはxに比例していない。（y=axの関係が成り立っていないため）

比例の式をグラフに

ではこれから比例の式を座標平面上に表してみましょう！

「座標平面って何？」という方は下のブログで！

////////////////////////////////////////////
「座標平面について」の
URLをここに貼る
/////////////////////////////////////////////

では前回の演習問題（３）の問題を用いて表とグラフを書きましょう。

比例の式は

$$y=\frac{3}{2}x$$

であるので、下の表を完成させましょう。

x座標	-4	-3	-2	-1	0	1	2	3	4
y座標

 

 

 

 

 

x座標	-4	-3	-2	-1	0	1	2	3	4
y座標	-6	$$-\frac{9}{2}$$	-3	$$-\frac{3}{2}$$	0	$$\frac{3}{2}$$	3	$$\frac{9}{2}$$	6

では上記の表を座標平面上にプロットしましょう。

これらの点を直線で結ぶと以下のようになる。

上記が比例におけるグラフになります。

ではグラフの書き方が分かったと思いますので、演習問題をやってみましょう。

次回は比例のグラフをもっと詳しく見ていきます。

 

演習問題

$$y=-2x$$

のグラフを描いてください。

解答は次のブログで！

//////////////////////////////////////////////////
ここに「比例のグラフ（その２）」のURLを貼る
//////////////////////////////////////////////////

 

前回(比例とは？)の解答

//////////////////////////////////////////////////
ここに「比例とは」のURLを貼る
//////////////////////////////////////////////////

時間[h]	0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
距離[km]	0	30	60	90	120	150	180	210	240

 

比例を式に！

では「比例とは」のブログで示した日常生活における例を式にし、グラフ化していきます。

なぜわざわざ式やグラフで表さなくてはならないのか。

これは時間を代入すると水の深さや移動した距離を簡単に求めることができ、とても簡単に結果を知ることができます。

また、グラフを書くことで時間と距離や長さの関係を視覚化し、よりわかりやすくすることができます。

比例の式　y=ax

まずは比例の式を覚えましょう。

$$y=ax$$

ではそれぞれの役割について見ていきましょう。

xは前記の具体例では時間を表します。

yは水の深さや移動した距離を表します。

aは「比例定数」と呼ばれ、歩く速度や水を入れる量を表します。

そしてxとyの関係がy=axとなるとき「yはxに比例する」と言います。

ここで注意する点として比例定数aはゼロにはならないことです。

例題

次の（１）～（３）についてyがxに比例するかどうか調べましょう。また比例するものについては、比例定数を求めなさい。

（１）1辺3x[cm]の正方形の面積をy[cm²]とする。
（２）1個300円のショートケーキをx個買う時の代金をy円とする。
（３）1000mの距離を秒速x[m]で走ったときにかかる時間をy秒とする。

解答

（１）
$$y=3x\times3x=9x^2$$
よってyはx²に比例し、yはxに比例していない。

（２）
$$y=300\times x=300x$$
よってyはxに比例し、比例定数は300となる。

（３）
$$y=1000\div x=\frac{1000}{x}$$
よってyはxに比例しない。

 

【演習問題】

次の問で、yがxに比例するかどうか調べましょう。また比例するものについては、比例定数を求めなさい。（３）は比例の式、比例定数とそれぞれの問に答えよ。

（１）半径3x[cm]の円の周の長さy[cm]

（２）分速100[m]でx分歩いた時の距離y[m]

（３）x=10の時、y=15である。
　　　x=4のときのyの値を求めよ。
　　　y=9のときのxの値を求めよ。

（４）長さx[cm]の正方形の面積y[cm²]

（５）一日の夜の長さx時間の時、朝と昼の長さy時間。